Экспоненциальная скользящая средняя ( Exponential Moving Average (EMA)), Экспоненциальное сглаживание

Экспоненциальную скользящую среднюю принято называть экспоненциальным сглаживанием. EMA является лучшей скользящей и технические аналитики предпочитают ее вместо других скользящих.

С точки зрения отношения к новым данным, EMA представляет превосходный компромис между повышенной чувствительностью взвешенной скользящей средней (WMA) и отставанием простой скользящей средней (SMA).

Сравнивая с другими техниками усреднения, EMA следует за трендом текущих данных гладко и плавно, минимизируя скачки и с наименьшим опозданием.

С точки зрения вычислений, EMA является самой простой и наиболее стремительной из всех техник скользящих средних. EMA требует небольшое количество расчетов, маленький обьем манипуляций с данными и меньше исторических данных. Для вычисления EMA, требуются данные только для двух периодов: самые последние данные и данные предшествующего периода EMA. Так работая с дневными данными, нам нужны только самые последние необработанные данные и вчерашние данные EMA. Таким образом EMA исключает возможность управлять большим обьемом исторических данных.

Существенным преимуществом этого вычислительного метода является то, что EMA никогда не исказит старые данные. Старые данные никогда не выпадают из расчета, поскольку не входят в него. На практике эффект последних данных постепенно уходит в соответствии с уменьшением веса вчерашней EMA.
Метод расчета EMA избегает проблему ошибок, связанных с ненужными и незначительными данными.

Экспоненциальная скользящая средняя рассчитывается так:
EMA = (C - Ep)K + Ep
где
EMA - Эсс для текущего периода.
C - Цена закрытия текущего периода.
Ep - Эсс предыдущего периода.
K - Экспоненциальная константа сглаживания равная 2 / (n + 1).
n - Количество периодов простого скользящего среднего в грубом приближении к Эсс.

Формула экспоненциальной постоянной сглаживания К = 2 / (n + 1) позволяет приблизительно сравнить любую EMA с более вялой простой скользящей средней длины n. С увеличением количества периодов n, величина K уменьшается, и Эсс становится менее чувствительной к новым данным.
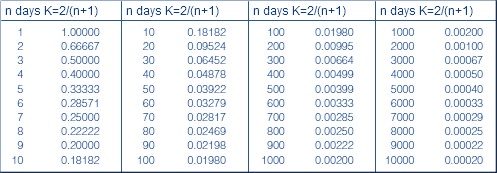
Используйте эту таблицу, чтобы соотнести число дней n с экспоненциальной константой сглаживания:



При первом расчете EMA, для точного значения необходимо учесть n дней. Для быстрого вычисления EMA, в первый день расчета мы можем использовать простую скользящую среднюю n дней, приблизительно равную Эсс за предшествующий период (Ep).

EMA = (C - Ep)K + Ep

После этого первого дня нам уже не понадобятся никакие данные, кроме Эсс за вчера и сегодняшние необработанные данные.

Таблица соотносит из простой n дней в экспоненциальную константу K дней, и наоборот.

Построение стратегии с экспоненциальной скользящей средней, 120 дней

Основанная на дневных ценах закрытия Dow-Jones index average с 1900 по 2001 года, стратегия экспоненциальной скользящей средней, длиной от 1 до 300 дней была прибыльной и опережала пассивную стратегию "купи и держи" на 69%.
Эсс длиной в 5, 3, 2 дня дала чистую прибыль выше 6 млрд. долларов, при начальном капитале в 100$ в 1900 году.
Все периоды Эсс от 1 до 20 дней приносили чистую прибыль более 10 млн. долларов; все 20 длин-стратегий превышали пассивную стратегию "купи и держи" в соотношении 540 к 1.

Все ЭСС длины периодов от 1 до 60 дней, дали чистую прибыль свыше одного миллиона долларов, а все 60 длин превзошли бы стратегию "купи и держи" более чем 64 к одному.

Из показателей длины, 44-дневная Эсс показала лучший результат, с чистой прибылью 3.251,721$, которая в 162 раза больше стратегии "купи и держи" на 20,105$.

Сумма падала с увеличением длины Эсс. Популярная стратегия в 200-дней Эсс принесла прибыль 109,158$, которая только в 5,4 больше стратегии "купи и держи" с 20,105$.

Из долгосрочных Эсс, т. е. тех чья длина превышает 100 дней, 120-дневная Эсс оказалась максимально выгодной и дает положительный результат, с максимальной прибылью, на исключительно механическом следовании за трендом, без субьективности, без применения сложных технических анализов.